GAMMAINV function in Excel, how to use and examples

With simple syntax, you can easily apply the GAMMAINV function to statistical problems.

Instructions on how to use the GAMMAINV function

Syntax : GAMMAINV(probability,alpha,beta)

In there :

- probability : Required – Is the probability associated with the gamma distribution.
- Alpha : Required – Is a parameter to the distribution.
- Beta : Required – Is a parameter to the distribution.

Consider the example

You enter into Excel the actual values ​​corresponding to the parameters of the GAMMAINV function in the excel cells. In this example, we calculate with the Probability associated with the gamma distribution is 0.0735, the Alpha Parameter of the distribution is 8 and the Alpha Parameter of the distribution is 3:

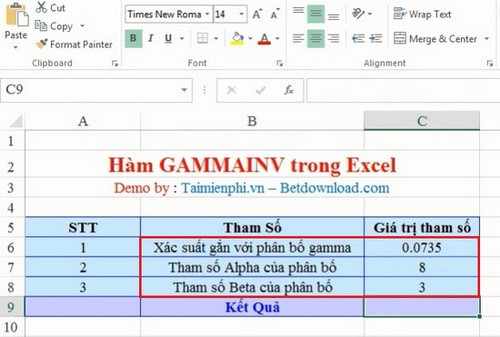
Enter the formula in cell C9. And the calculated result of the function is 13.00013994:

So now you know how to use the GAMMAINV function in Excel to calculate the inverse value of the cumulative gamma distribution. When the Beta parameter is 1, the function will return the standard gamma distribution, otherwise if Beta is not positive, Excel will display the #NUM! error.

The GAMMAINV function is supported on many versions such as Office 2013, Office 2010, Office 2007 and Office 2003, helping users easily apply it to probability analysis and data statistics problems. You can also combine it with functions such as GAMMADIST to analyze distributions more accurately.