Summary of technical functions in Excel

The following article introduces in detail the technical functions in excel.

 

1. CONVERT function

Description: The function converts back and forth between measurement units. For example, converting units in weight, mass, length, time, energy .

Syntax: CONVERT (number, from_unit, to_unit) .

Inside:

- number: the value you want to convert.

- from_unit: The original unit of value you want to convert.

- to_unit: The unit of measurement you want to convert to.

For example: Convert (5, g, ozm): Convert 5g to Ounce mass units.

Standard for writing conversion units:

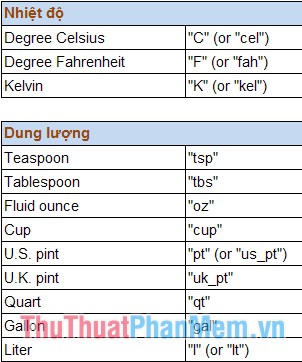
2. BESSELI function

Description: Returns the BESSELI function of the In (x) transform.

Syntax: BESSELI (x, n) .

Inside:

- x is the value to calculate the Besseli function.

- n is the order of the function, if n is a decimal number => the function takes the rounding value of n.

Attention:

- If n function returns the value #NUM!

- x, n must be numeric values ​​if entered incorrectly => #VALUE error message.

Example: BESSELI (2.5,3) => Variable Besseli function In (x) first order at value 1.5 => result = 0.47437.

3. The BESSELJ function

Description: Returns the BESSELJ function of the variable Jn (x).

Syntax: BESSELJ (x, n) .

Inside:

- x is the value to calculate the Besselj function.

- n is the order of the function, if n is a decimal number => the function takes the rounding value of n.

Attention:

- If n function returns the value #NUM!

- x, n must be numeric values ​​if entered incorrectly => #VALUE error message.

For example: BESSELJ (2.5,3) => The Besselj function transforms first-degree jn (x) at value 1.5 => result = 0.2166.

4. The BESSELK function

Description: Returns the BESSELK function of the Kn (x) transform.

Syntax: BESSELK (x, n) .

Inside:

- x is the value to calculate the Besselk function.

- n is the order of the function, if n is a decimal number => the function takes the rounding value of n.

Attention:

- If n function returns the value #NUM!

- x, n must be numeric values ​​if entered incorrectly => #VALUE error message.

Example: BESSELK (2.5,3) => Variable Besselk function In (x) first order at value 1.5 => result = 0.268227.

5. BESSELY function

Description: Returns the BESSELY function of the variable Yn (x).

Syntax: BESSELY (x, n) .

Inside:

- x is the value to calculate the Bessely function.

- n is the order of the function, if n is a decimal number => the function takes the rounding value of n.

Attention:

- If n function returns the value #NUM!

- x, n must be numeric values ​​if entered incorrectly => #VALUE error message.

For example: BESSELY (2.5,3) => The Bessely function transforms Yn (x) first order at the value 1.5 => result = -0.75605.

6. The BIN2DEC function

Description: The function performs conversion of binary numbers to decimal numbers.

Syntax: BIN2DEC (number) .

Inside:

number is the value to convert.

Note: If number is more than 10 characters => function value returns an error! NUM.

7. DEC2BIN function

Description: The function performs conversion of decimal values ​​to numbers in binary.

Syntax: DEC2BIN (number [, places]) .

Inside:

- number is the value to convert, places arbitrary parameters.

- places is the number of characters you want to use in the return value.

8. The BIN2HEX function

Description: The function performs a number conversion from binary to hexadecimal.

Syntax: BIN2HEX (NUMBER [, PLACE]) .

Inside:

- Number is the binary value you want to convert.

- Place (the arbitrary value): is the number of characters of the returned result, if omitted excel, get the minimum number of characters enough to return the result.

Attention:

- Place is a natural and non-negative numerical value.

- If the value you want to convert is more than 10 characters => the #NUM !.

- If the conversion value is negative, the function ignores the place parameter and returns the result with 10 characters in hexadecimal.

- If the result has a larger number of characters than the specified in place => error #Num!

- If you enter place as a decimal value, get the integer part of the place.

9. Ham HEX2BIN

Description: The function performs conversion of numeric values ​​from hexadecimal to binary.

Syntax: HEX2BIN (number [, place]) .

Inside:

- number is the value you want to convert.

- place: arbitrary value, specifying the number of characters of the returned result.

Attention:

- Enter the number value in quotation marks eg HEX2BIN ("F").

10. BIN2OCT function

Description: The function converts binary numbers to octal numbers.

Syntax: BIN2OCT (number [, places]) .

Where: number is the value you want to convert, place is an arbitrary value that is the number of characters of the returned result.

Note: Notes are similar to the above functions.

11. OCT2BIN function

Description: The function converts numbers from octal to binary.

Syntax: OCT2BIN (number [, places]) .

Inside:

- number is the value to be converted.

- places: number of characters of the returned result, arbitrary parameters, if omitted excel, the minimum value is sufficient to denote the result.

Note: Notes are similar to the above conversion functions.

12. Ham COMPLEX

Description: The function converts real and imaginary factors into complex numbers of the form x + yi or x + ỵ.

Syntax: COMPLEX (real_num, i_num [, suffix] .

Inside:

- real_num: real coefficient is a numerical value.

- i_num: The imaginary coefficient is a numerical value.

- suffix: suffix of virtual coefficient of complex number if ignoring default is i, if not put in quotation marks.

Note: If 1 of 2 real_num and i_num values ​​are not numeric => #Value error. Or, in case of input suffix outside the characters i and j, the error function #Value.

13. The DEC2OCT function

Description: Convert decimal numbers to octal numbers.

Syntax: DEC2OCT (number, places) .

Inside:

- number: is the decimal number to be converted to octal.

- places: is the number of characters of the returned result. If you enter places, the return result contains the leading zero if the result has fewer characters than places.

Attention:

- If number> 536,870,911 or number <-536870912, or places exceeds 40 characters or places the #NUM!

- If number, places are not numbers => the error message #VALUE!

14. The DELTA function

Description: Check if the 2 numbers are equal or not.

Syntax: DELTA (number 1, number 2) .

Inside:

- number1: is the 1 comparison value.

- number2: is the second comparison value.

If two values ​​are equal => the value of the function returns 1, otherwise it returns 0.

Note: 2 values ​​must be numeric values, if the error value type is entered in the #VALUE error function.

15. GESTEP function

Description: How the function is used to compare 2 values.

Syntax: GETSTEP (number, step) .

Inside:

- number is the value to compare.

- step: value to compare.

If number> step => GETSTEP returns 1, otherwise number

Attention:

- If you do not enter the test value, step by step the function automatically understands the value of step = 0.

- The two parameters of the function must be a numeric value otherwise the #VALUE error function will be displayed.

16. The IMAGINARY function

Description: The function returns the imaginary coefficient of a real number in a complex coefficient.

Syntax: IMAGINARY (number) .

Inside:

- number is a complex number to get a virtual coefficient.

17. IMDIV function

Description: The function performs the quotient of 2 complex numbers.

Syntax: IMDIV (inumber1, inumber2) .

Inside:

- inumber1 is the first complex number to be calculated.

- inumber2 is the second complex number to be calculated.

18. IMLN function

Description: The function performs the natural logarithm of a complex number.

Syntax: IMLN (inumber) .

Inside:

- inumber is a complex number that needs to be calculated naturally.

19. The IMLOG2 function

Description: The function performs base 2 logarithms of a complex number.

Syntax: IMLOG2 (inumber) .

Inside:

- inumber is a complex number to be calculated base 2's logarithm.

20. IMPRODUCT function

Description: The function performs the product of the product of 2 complex numbers.

Syntax: IMPRODUCT (inumber1, inumber2, inumber3, .) .

Inside:

- inumber are complex numbers to calculate.

Note: Complex numbers entered in quotation marks.

For example, IMPRODUCT ("3-2i", "24-9i").

21. IMSIN function

Description: The function performs calculating the sine value of a complex number.

Syntax: IMSIN (number) .

Inside:

- number is a complex number to be calculated.

22. IMSUB function

Description: The function performs the difference of two complex numbers.

Syntax: IMSUB (inumber1, inumber2) .

Inside:

- inumber1 is the first complex number.

- inumber 2 is the second complex number.

23. The IMABS function

Description: Calculate the absolute value of a complex number.

Syntax: IMABS (inumber) .

Inside:

- inumber is a complex number that needs absolute value calculation.

24. IMEXP function

Description: The function performs exponentiation e of complex numbers.

Syntax: IMEXP (inumber) .

Inside:

- inumber is a complex number whose base power is to be calculated e.

25. IMCOS function

Description: Perform the cosine calculation of a complex number.

Syntax: IMCOS (inumber) .

Inside:

- inumber is a complex number for cosine.

Note: The value of entering a complex number is enclosed in quotation marks.

26. IMLOG10 function

Description: The function performs base 10 logarithms of a complex number.

Syntax: IMLOG10 (inumber) .

Inside:

- inumber is a complex number to be calculated base 10 logarithms.

27. IMPOWER function

Description: The function performs exponentiation of a complex number.

Syntax: IMPOWER (inumber, number) .

Inside:

- number is a complex number for exponentiation, number is exponent.

28. The function IMREAL

Description: The function that performs the calculation returns the real coefficient of the complex number.

Syntax: IMREAL (inumber) .

Inside:

- inumber is a complex number to find the real coefficient.

Note: Enter a complex numeric value in quotation marks.

For example: IMREAL ("15-6i").

29. IMSQRT

Description: The function performs the square root of a complex number.

Syntax: IMSQRT (inumber) .

Inside:

- inumber is a complex numerical value to calculate square root.

30. IMSUM function

Description: The function performs calculations and returns the total value of 2 complex numbers.

Syntax: IMSUM (inumber1, inumber2, inumber3, .) .

Inside:

- inumber is complex numbers to be calculated with complex numbers to calculate up to 29 numbers.