Displaystyle: How to Calculate Slope and Intercepts of a Line

This updated guide examines Displaystyle: How to Calculate Slope and Intercepts of a Line and organizes the essential facts, background, and practical takeaways in clear American English.

Method 1

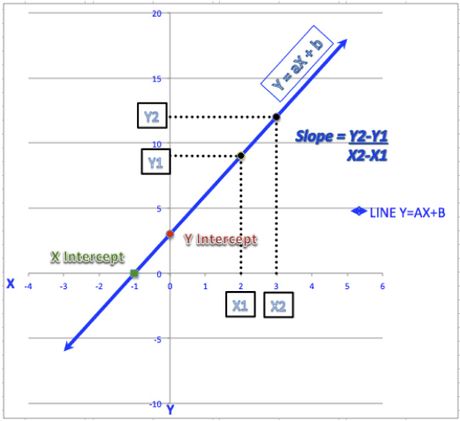
Using a Graph to Find the Slope

1. Pick two points on the line. Draw dots on the graph to represent these points, and note their coordinates.
   • Remember when graphing points to list the x-coordinate first, then the y-coordinate.
   • For example, you might choose the points (-3, -2) and (5, 4).
2. Determine the rise between the two points. To do this, you must compare the difference in y of the two points. Begin with the first point, the point that is the farthest left on the graph, and count up until you reach the y-coordinate of the second point.
   • The rise can be positive or negative; that is, you can count up or down to find it.^[4]If the line is moving up and to the right, the rise is positive. If the line is moving down and to the right, the rise is negative.^[5]
   • For example, if the y-coordinate of the first point is (-2), and the y-coordinate of the second point is (4), you will count up 6 points, so your rise is 6.
3. Determine the run between the two points. To do this, you must compare the difference in x of the two points. Begin with the first point, the point that is farthest left on the graph, and count over until you reach the x-coordinate of the second point.
   • To run is always positive; that is, you can only count from left to right, never right to left.^[6]
   • For example, if the x-coordinate of the first point is (-3), and the x-coordinate of the second point is (5), you will count over 8, so your run is 8.
4. Make a ratio using the rise over the run to determine the slope. The slope is usually in fraction form, but it can also be a whole number.
   • For example, if the rise is 6 and the run is 8, then your slope is68{displaystyle {frac {6}{8}}}, which can be simplified to34{displaystyle {frac {3}{4}}}.

Method 2

Using Two Given Points to Find the Slope

1. Set up the formulam=y2?y1x2?x1{displaystyle m={frac {y_{2}-y_{1}}{x_{2}-x_{1}}}}. In the formula, m = the slope,(x1,y1){displaystyle (x_{1},y_{1})}= the coordinates of the first point,(x2,y2){displaystyle (x_{2},y_{2})}= the coordinates of the second point.
   • Remember that the slope is equal toriserun{displaystyle {frac {rise}{run}}}. You are using this formula to find the change in y (rise) over the change in x (run).^[7]
2. Plug the x- and y-coordinates into the formula. Make sure you place the coordinates of the first point ((x1,y1){displaystyle (x_{1},y_{1})}) and the second point ((x2,y2){displaystyle (x_{2},y_{2})}) in the correct positions in the formula, or else you will not calculate the correct slope.
   • For example, given the points (-3, -2) and (5, 4), your formula will look like this:m=4?(?2)5?(?3){displaystyle m={frac {4-(-2)}{5-(-3)}}}.
3. Complete the calculation and simplify, if possible. This will give you the slope as a fraction or whole number.
   • For example, if your slope ism=4?(?2)5?(?3){displaystyle m={frac {4-(-2)}{5-(-3)}}}you should calculate4?(?2)=6{displaystyle 4-(-2)=6}in the numerator (Remember when subtracting a negative number, you add.) and5?(?3)=8{displaystyle 5-(-3)=8}in the denominator. You can simplify68{displaystyle {frac {6}{8}}}to34{displaystyle {frac {3}{4}}}, som=34{displaystyle m={frac {3}{4}}}.

Method 3

Finding the y-intercept, Given the Slope and One Point

1. Set up the formulay=mx+b{displaystyle y=mx+b}. In the formula, y = the y-coordinate of any point on the line, m = slope, x = the x-coordinate of any point on the line, and b = the y-intercept.
   • y=mx+b{displaystyle y=mx+b}is the equation of a line.^[8]
   • The y-intercept is the point at which the line crosses the y-axis.
   EXPERT TIPMath Instructor, City College of San Francisco Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University.Grace Imson, MA Math Instructor, City College of San Francisco

   Our Expert Agrees: If you have the slope and one point, plug them into the equation of the line. In y = mx + b, m is the slope, and the point coordinate will contain both x and y. Then, solve for b to find the y-intercept.

2. Plug in the slope and the coordinates of one point in the line. Remember, the slope is equal to the rise over the run. If you need help finding the slope, see the instructions above.
   • For example, if the slope is34{displaystyle {frac {3}{4}}}, and on point on the line is (5,4), then the formula will look like this:4=34(5)+b{displaystyle 4={frac {3}{4}}(5)+b}.
3. Complete the equation, solving for b. First multiply the slope and the x-coordinate. Subtract this number from both sides to solve for b.
   • In the example problem the equation becomes4=334+b{displaystyle 4=3{frac {3}{4}}+b}. Subtracting334{displaystyle 3{frac {3}{4}}}from both sides, you end up with14=b{displaystyle {frac {1}{4}}=b}. So the y-intercept is14{displaystyle {frac {1}{4}}}.
4. Check your work. On a coordinate graph, plot your known point, then draw a line using the slope. To find the y-intercept, look for the point where the line crosses the y-axis.
   • For example, if the slope is34{displaystyle {frac {3}{4}}}, and one point is (5,4), draw a point at (5,4), then draw other points along the line by counting to the left 3 and down 4. When you draw a line through the points, you should see the line cross the y-axis just above the (0,0) coordinate.

Method 4

Finding the x-intercept, Given the Slope and Y-intercept

1. Set up the formulay=mx+b{displaystyle y=mx+b}. In the formula, y = the y-coordinate of any point on the line, m = slope, x = the x-coordinate of any point on the line, and b = the y-intercept.
   • y=mx+b{displaystyle y=mx+b}is the equation of a line.^[9]
   • The x-intercept is the point at which the line crosses the x-axis.
2. Plug the slope and y-intercept into the formula. Remember, the slope is equal to the rise over the run. If you need help finding the slope, see the instructions above.
   • For example, if the slope is34{displaystyle {frac {3}{4}}}, and the y-intercept is14{displaystyle {frac {1}{4}}}, the formula will look like this:y=34x+14{displaystyle y={frac {3}{4}}x+{frac {1}{4}}}.
3. Set y to 0. ^[10]You are looking for the x-intercept, the point at which the line crosses the x-axis. At this point, the y-coordinate will equal zero. So if we set y to 0, and solve for the corresponding x-coordinate, we will find the point (x, 0), which will be the x-intercept.
   • In the example problem, the equation becomes0=34x+14{displaystyle 0={frac {3}{4}}x+{frac {1}{4}}}.
4. Complete the equation, solving for x. First subtract the y-intercept from both sides. Then divide both sides by the slope.
   • In the example problem the equation becomes?14=34x{displaystyle {frac {-1}{4}}={frac {3}{4}}x}. Dividing both sides by34{displaystyle {frac {3}{4}}}, you end up with?412=x{displaystyle {frac {-4}{12}}=x}. This simplifies to?13=x{displaystyle {frac {-1}{3}}=x}. So the point at which the line crosses the x-axis is(?13,0){displaystyle ({frac {-1}{3}},0)}. So the x-intercept is?13{displaystyle {frac {-1}{3}}}.
5. Check your work. On a coordinate graph, plot your y-intercept, then draw a line using the slope. To find the x-intercept, look for the point where the line crosses the x-axis.
   • For example, if the slope is34{displaystyle {frac {3}{4}}}, and the y-intercept is(0,14){displaystyle (0,{frac {1}{4}})}, draw a point at(0,14){displaystyle (0,{frac {1}{4}})}, then draw other points along the line by counting to the left 3 and down 4, and to the right 3 and up 4. When you draw a line through the points, you should see the line cross the x-axis just left of the (0,0) coordinate.
6. Final Image: