Heap data structure

What is the Heap data structure?

Data structure The heap is a special case of a balanced binary tree data structure, where the root node's key is compared to its children and arranged accordingly. If α has a child node β then:

key (α) ≥ key (β)

When the value of the parent node is greater than the value of the child node, this attribute creates a Max Heap. Based on this criterion, a Heap can be one of two types:

 With data filled in → 35 33 42 10 14 19 27 44 26 31 

Min-Heap : here the value of the root node is less than or equal to the values ​​of the child nodes.

Max-Heap : here the value of the root node is greater than or equal to the value of the child nodes.

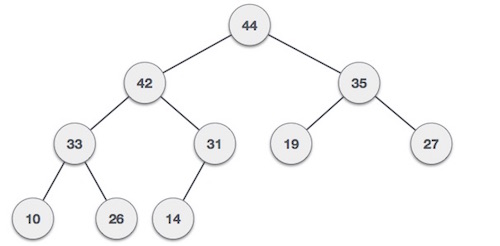
The above two example trees are all built on the same input data and the same order.

Max Heap construction algorithm

We will use the same example to illustrate how to create a Max Heap. The method to build Min Heap is similar.

We will deduce an algorithm for Max Heap by inserting an element at a time. At any time, Heap must maintain (obey) its properties. During the insert process, we also assume that we are inserting a node in HEAPIFIED Tree.

 Bước 1 : Tạo một nút mới tại vị trí cuối cùng của Heap. Bước 2 : Gán giá trị mới cho nút này. Bước 3 : So sánh giá trị của nút con với giá trị cha. Bước 4 : Nếu giá trị của cha là nhỏ hơn con thì tráo đổi chúng. Bước 5 : Lặp lại bước 3 và 4 cho tới khi vẫn duy trì thuộc tính của Heap.

Note : In the Min Heap build algorithm, the value of the parent node will be smaller than the value of the child nodes.

For more details on Max Heap construction algorithm, let's look at the animated illustration below.

The algorithm deletes in Max Heap

Delete operation in Max (or Min) Heap always takes place at the root node and to delete the Largest (or Smallest) value. You follow the algorithm and animation below to understand more about this algorithm.

 Bước 1 : Xóa nút gốc. Bước 2 : Di chuyển phần tử cuối cùng có bậc thấp nhất lên nút gốc. Bước 3 : So sánh giá trị của nút con này với giá trị của cha. Bước 4 : Nếu giá trị của cha là nhỏ hơn của con thì tráo đổi chúng. Bước 5 : Lặp lại bước 3 và 4 cho tới khi vẫn duy trì thuộc tính của Heap.

According to Tutorialspoint

Previous article: Spanning Tree in data structure and algorithm

Next lesson: Basics of recursion