Binary Search algorithm (Binary Search)

What is binary search algorithm (Binary Search)?

Binany Search is a fast search algorithm with runtime complexity of Ο (log n). The algorithm of binary search works based on the principle of division and rule (Divide and Conquer). In order for this algorithm to work correctly, the data set should be in sorted form.

Binary Search searches for a specific element by comparing the element at the middle of the data set. If a connection is found, the index of the element is returned. If the required element is greater than the middle element value, the element to be found is found in the sub-array to the right of the middle element; otherwise, look in the sub-array to the left of the middle element. The process will continue on the sub array until all elements in this sub array are found.

The way Binary Search works

In order for Binary Search to work, the array must be sorted. For ease of tracking, I will provide more illustrations corresponding to each step.

Suppose we need to find the location of value 31 in an array that includes the values ​​shown below using Binary Search:

First, we divide the array into two halves according to the following operation:

 only-item-middle = board-start + (end + initial) / 2 

With the above example is 0 + (9 - 0) / 2 = 4 (value is 4.5). Therefore 4 is the middle index of the array.

Now we compare the element value between the element to find. The middle element value is 27 and the search element is 31, so there is no connection. Because the value to be searched for is larger, the element to be found is in the sub-array to the right of the middle element.

We change the initial-value to just-item-between + 1 and again search for the middle-only-item value.

 original-first = only-item-middle + 1 
 only-item-middle = board-start + (end + initial) / 2 

Now our middle index is 7. We compare the value in this index to the value to search.

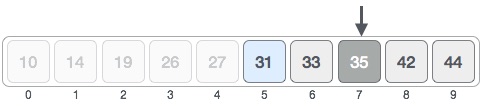
The value in index 7 is not connected, and in addition, the value to look for is less than the value in index 7 so we need to look in the sub-array to the left of this index.

Continue to find the middle-item again. This time it's worth 5.

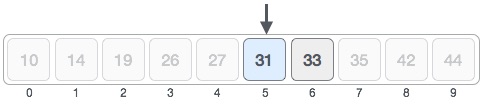
Compare the value in index 5 with the value to find and find that it connects.

Therefore we conclude that the value to be searched for is stored at index position 5.

Binary Search bisects the number of elements needed and thus reduces the number of comparisons that need to be performed, so this search algorithm is done quite quickly.

Sample algorithm for Binary Search

Below is the sample code for binary search algorithm:

 Binary Search algorithm (Binary Search) 
 A ← an array has been sorted 
 n ← array size 
 x ← value to search in the array 

 assign lowerBound = 1 
 assign upperBound = n 

 trong khi x không tìm thấy 

 if upperBound  EXIT: x does not exist. 

 assign midPoint = lowerBound + (upperBound - lowerBound) / 2 

 if A [midPoint]  assign lowerBound = midPoint + 1 

 if A [midPoint]> x 
 assign upperBound = midPoint - 1 

 if A [midPoint] = x 
 EXIT: x is found at midPoint 

 while end 

 End the algorithm 

According to Tutorialspoint

Previous article: Linear search algorithm (Linear Search)

Next lesson: Interpolation Search algorithm (Interpolation Search)