BINOM.DIST function - Function returns the probability of binomial distribution of individual terms in Excel

The following article introduces you to the BINOM.DIST function - one of the functions in the statistical function group is very popular in Excel.

Description: The function returns the binomial distribution probability of the individual term. Support function from Excel 2010 version.

Syntax: BINOM.DIST (number_s, trials, probability_s, cumulative)

Inside:

- number_s: number of successes in the test, a required parameter.

- trials: Number of independent trials, required.

- probability_s: The probability of success of each test, is a required parameter.

- cumulative: Logical value determines the form of the function if it is True -> returns the cumulative distribution function, if the False value returns the probability mass function .

Attention:

- If number_ s and trials are not whole numbers they are truncated to whole numbers.

- If number_ s and trials are not numbers -> the function returns the #VALUE! Error value

- If number_s <0 or number_s > trials -> the function returns the #NUM! Error value 

- If probability_s <0 or probability_s> 1 -> the function returns the #NUM! Error value 

- Binomial probability function is:

[bleft ({x, n, p} right) = left ({begin {array} {* {20} {c}}
n
x
end {array}} right) {p ^ N} {left ({1 - p } right) ^ {n - N}}]

Inside:

(left ({begin {array} {* {20} {c}} nx end {array}} right)): COMBIN (n, x).

- Cumulative binomial distribution function is:

[Bleft ({x, n, p} right) = sumlimits_ {y = 0} ^ N {bleft ({y, n, p} right)}]

For example:

Calculate the probabilities of the tests with the data in the table below:

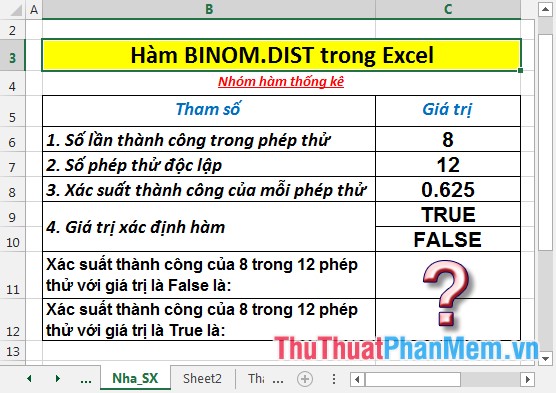
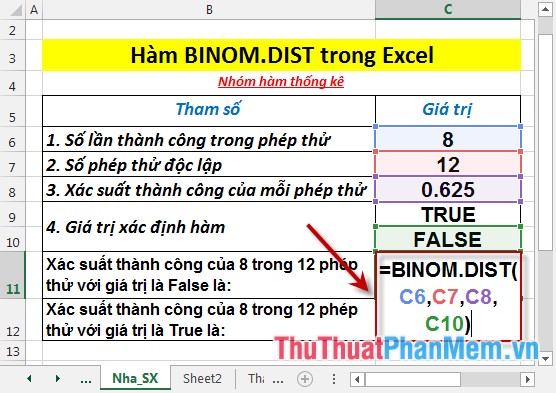
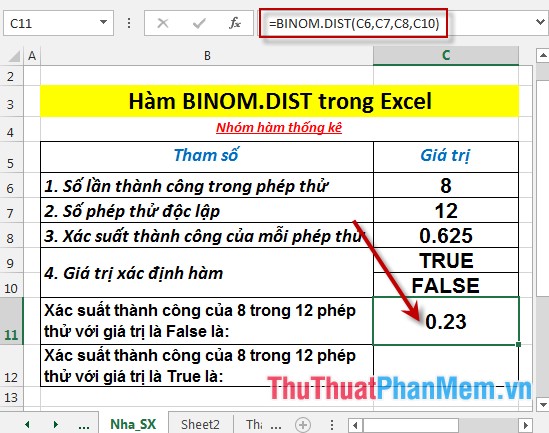
- Calculate the probability of success in 8 of the 12 tests with a value of False. In the cell to calculate enter the formula : = BINOM.DIST (C6, C7, C8, C10)

- Press Enter -> probability of success is:

- Calculate the probability of success in 8 of the 12 tests with a value of True. In the cell to calculate enter the formula : = BINOM.DIST (C6, C7, C8, C9)

- Press Enter -> probability of success is:

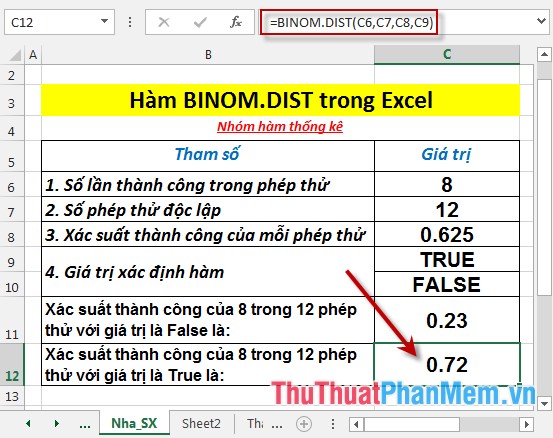
So with different function defined values ​​-> the function returns the same result.

Above are instructions and specific examples when using the BINOM.DIST function in Excel.

Good luck!