Recursive function in Python

In previous Python articles, you learned about Python functions, built-in Python functions, and user-defined Python functions. In this article we will learn more about recursive functions in Python, which call itself, as well as how to create recursive functions and examples.

What is the recursive function in Python?

Recursion is a way to program or code a problem, in which the function calls itself once or more times in the code block. Usually, it returns the return value of the function call. If the function definition satisfies the recursive condition, the function is called a recursive function.

Condition terminated: A recursive function must have conditional termination to stop calling itself back. Recursive functions cease when each recursive call has reduced the number of solutions to the base condition. A basic condition is the point at which the problem is solved and no further recursion is required. If recursive calls cannot reach the base condition, the recursive function becomes an infinite loop.

Thus, it can be said that recursion in computer science is a method of solving problems based on solving smaller cases of the same problem.

In Python, the recursive function is similar, can call itself and has a base condition for recursive termination.

Examples of recursive functions in Python

The most classic example of recursive function is the factorial of an integer. The factorial of a number is the result of multiplication from one to that number. For example, 5 factorials (written as 5!) Are 1 * 2 * 3 * 4 * 5 = 120.

In Python, the factorial of a number is written as follows:

 def giaithua(n): 
 """Đây là hàm tính giai thừa của 
 một số nguyên by TipsMake.com""" 
  if n == 1: 
 return 1 
 else: 
 return (n * giaithua(n-1)) 
 num = 5 
 num1 = int(input("Nhập số cần tính giai thừa: ")) 
 print("Giai thừa của", num, "là", giaithua(num)) 
 print("Giai thừa của", num1, "là", giaithua(num1)) 
 

In the above example, look at the definition of the function giaithua(n) , in the if . else statement, the giaithua(n) function giaithua(n) has called itself again. Run the above code and get the following result:

Recursive function in Python Picture 1

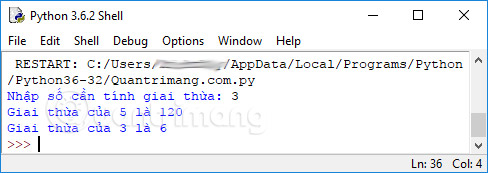
When calling the function giaithua(n) with a positive integer, it will call recursively by decreasing the number. Each time the function is called, it multiplies the number with the factorial of 1 until the number equals 1. This recursive call can be explained in the following steps:

 giaithua (4) # The first call with 4 
 4 * giaithua (3) # Second call with 3 
 4 * 3 * giaithua (2) # The third call with 2 
 4 * 3 * 2 * giaithua (1) # The fourth call with 1 
 4 * 3 * 2 * 1 # Returned from call 4 when number = 1 
 4 * 3 * 2 # Returned from call 3 
 4 * 6 # Return from call 2 
 24 # Returns from the first call 

The recursion ends when the number drops to 1. This is called the base condition. Each recursive function must have a basic condition to stop recursion or it will become an infinite function, calling itself to it.

Advantages of recursive functions:

1. Recursive functions make the code look leaner and softer.
2. Complex tasks can be divided into simpler problems using recursion.
3. Creating sequences with recursion is easier than using nested loops.

Disadvantages of recursion:

1. Sometimes the logic behind recursion is quite difficult to understand.
2. Call recursion is expensive (ineffective) because they take up a lot of memory and time.
3. Recursive functions are difficult to debug.

Each recursive function calls itself stored on memory. Therefore, it consumes more memory than traditional functions. Python will stop calling the function after 1000 calls. If you run the code below:

 def giaithua(n): 
 """Đây là hàm tính giai thừa của 
 một số nguyên by TipsMake.com""" 
  if n == 1: 
 return 1 
 else: 
 return (n * giaithua(n-1)) 
 
 print (giaithua(1001)) 

Will receive an error message:

 RecursionError: maximum recursion depth exceeded in comparison 

This problem can be solved by adjusting the number of recursive calls, as follows:

 import sys 
 sys.setrecursionlimit(5000) 
 
 def giaithua(n): 
 """Đây là hàm tính giai thừa của 
 một số nguyên by TipsMake.com""" 
  if n == 1: 
 return 1 
 else: 
 return (n * giaithua(n-1)) 
 
 print (giaithua(1001)) 

But remember, there is still an input limit for factorial functions. For this reason, you should use recursion wisely. To calculate factorial, recursion is not the best solution, for other issues such as directory traversing (traversing a directory), recursion is a good solution.

Python recursive lesson stops here. In the next lesson, we will learn about the Python / Anonymous function / Python function, so don't miss it.

Do not forget to store your Python files.

Next lesson: Anonymous function, Lambda in Python

Previous post: Python function parameter