Spanning Tree in data structure and algorithm

What is a Spanning Tree?

A spanning tree is a subset of Grahp G that has all vertices enclosed by the minimum number of edges. Therefore, a spanning tree will not form a cycle and it cannot be interrupted in the middle.

From the above definition we can conclude that each periodic Graph G will have at least one spanning tree. A broken Graph G will not have any spanning trees.

Below is an example of an example of a Ghp and its spanning trees:

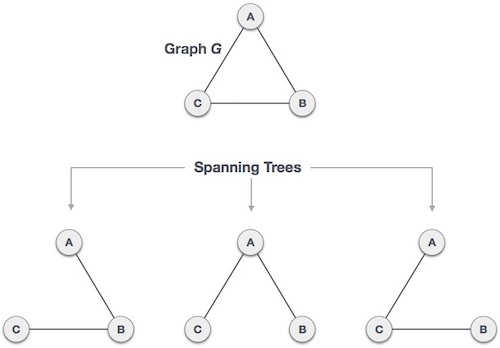
Spanning Tree in data structure and algorithm Picture 1

Above we have 3 spanning trees of a periodic graph. A periodic graph can have up to n ^n-2 spanning trees, where n is the number of nodes. In the above example, n is 3 so 3 ³⁻² = 3 spanning trees.

Common properties of the spanning tree (Spanning Tree)

We now understand that a Graph can have more than one spanning tree. The following are some of the properties of the cyclic Graph G tree given:

A periodic Ghp can have more than one spanning tree.

All spanning trees of a Graph G have the same number of edges and vertices.

The spanning tree does not have any cycles.

Removing an edge from a spanning tree will cause the Grahp to be non-periodic.

Adding an edge to the spanning tree creates a cycle.

Mathematical properties of the spanning tree (Spanning Tree)

The spanning tree has n-1 edges, where n is the number of nodes (vertices).

From a periodic Graph, by deleting the maximum of e-n + 1 edges, we can construct a spanning tree.

A recurring grahp can have up to n ^n-2 spanning trees.

Application of the frame tree (Spanning Tree)

Basically, the spanning tree is used to find the shortest path to connect all nodes in a Graph. Common applications of spanning trees are:

Civil network planning
Computer network routing protocol
Cluster Analysis

We explore the following simple example to understand these applications. Imagine an internet in the city as a large graph and now the plan is to deploy network lines so that the shortest wire length can still connect all the nodes. city. That is an example explanation for the application of the spanning tree.

Minimum Spanning Tree (MST)

In a Weighted Graph, a minimum spanning tree is a spanning tree that has the smallest weight of all these Grahp spanning trees. In real life, the weight here can be distance (distance), congestion, traffic load, or any value that can be represented as edges.

Algorithms for the smallest spanning tree

Because of the page length limitation, I will not present the following two algorithms in this chapter. Please click on the following two links to further explore the two most important spanning tree algorithms:

The smallest spanning algorithm of Kruskal
The smallest arithmetic algorithm of Prim

According to Tutorialspoint

Previous article: AVL tree in data structure and algorithm

Next lesson: Heap data structure

Spanning Tree

Micah Soto

Update 25 May 2019

You should read it

May be interested

Heap data structure
data structure the heap is a special case of a balanced binary tree data structure, where the root node's key is compared to its children and arranged accordingly.
Selection sort algorithm (Selection Sort)
selection sort is a simple algorithm. this sorting algorithm is an algorithm based on in-place comparison, in which the list is divided into two parts, sorted (list) on the left and unsorted (unsorted list) in the right. initially, the sorted part is blank and the unordered part is the original list.
Basics of recursion (Recursion)
some programming languages allow a module or function to be called to itself. this technique is called recursion.
Problem of Hanoi Tower (Tower of Hanoi)
problem of hanoi tower (tower of hanoi) is a math game consisting of 3 columns and with more disk numbers 1.
Alignment algorithm (Merge Sort)
mixing (merge sort) is an arrangement algorithm based on the divide and conquer algorithm. with the worst case time complexity of Ο (n log n), this is one of the algorithms that deserves the most attention.
Shell Sort in data structure and algorithm
shell sort is a highly efficient sorting algorithm based on insertion sorting algorithm (insertion sort). this algorithm avoids the case of swapping positions of two distant elements in the selection algorithm (if the smaller element is in the right position quite far from the larger element on the left).