HomeProgramData structure and algorithm

Heap data structure

What is the Heap data structure?

Data structure The heap is a special case of a balanced binary tree data structure, where the root node's key is compared to its children and arranged accordingly. If α has a child node β then:

key (α) ≥ key (β)

When the value of the parent node is greater than the value of the child node, this attribute creates a Max Heap. Based on this criterion, a Heap can be one of two types:

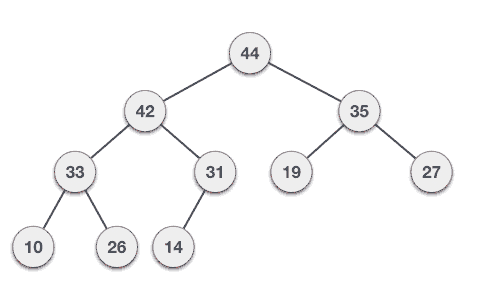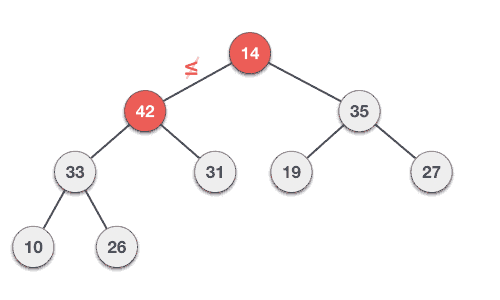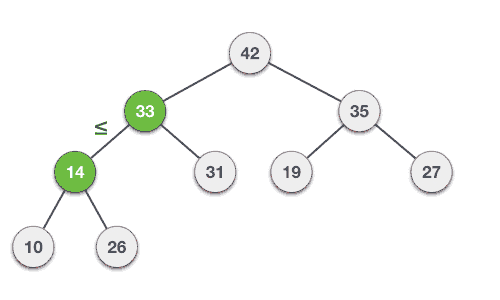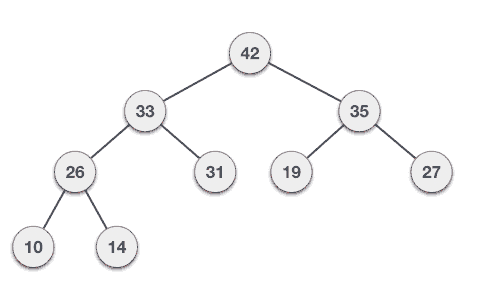
 With data filled in → 35 33 42 10 14 19 27 44 26 31

Min-Heap : here the value of the root node is less than or equal to the values ​​of the child nodes.

Heap data structure Picture 1

Max-Heap : here the value of the root node is greater than or equal to the value of the child nodes.

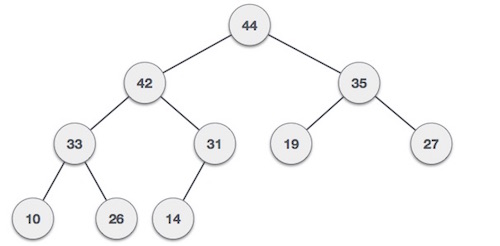
Heap data structure Picture 2

The above two example trees are all built on the same input data and the same order.

Max Heap construction algorithm

We will use the same example to illustrate how to create a Max Heap. The method to build Min Heap is similar.

We will deduce an algorithm for Max Heap by inserting an element at a time. At any time, Heap must maintain (obey) its properties. During the insert process, we also assume that we are inserting a node in HEAPIFIED Tree.

 Bước 1 : Tạo một nút mới tại vị trí cuối cùng của Heap. Bước 2 : Gán giá trị mới cho nút này. Bước 3 : So sánh giá trị của nút con với giá trị cha. Bước 4 : Nếu giá trị của cha là nhỏ hơn con thì tráo đổi chúng. Bước 5 : Lặp lại bước 3 và 4 cho tới khi vẫn duy trì thuộc tính của Heap.

Note : In the Min Heap build algorithm, the value of the parent node will be smaller than the value of the child nodes.

For more details on Max Heap construction algorithm, let's look at the animated illustration below.

Heap data structure Picture 3

The algorithm deletes in Max Heap

Delete operation in Max (or Min) Heap always takes place at the root node and to delete the Largest (or Smallest) value. You follow the algorithm and animation below to understand more about this algorithm.

 Bước 1 : Xóa nút gốc. Bước 2 : Di chuyển phần tử cuối cùng có bậc thấp nhất lên nút gốc. Bước 3 : So sánh giá trị của nút con này với giá trị của cha. Bước 4 : Nếu giá trị của cha là nhỏ hơn của con thì tráo đổi chúng. Bước 5 : Lặp lại bước 3 và 4 cho tới khi vẫn duy trì thuộc tính của Heap.

Heap data structure Picture 4

According to Tutorialspoint

Previous article: Spanning Tree in data structure and algorithm

Next lesson: Basics of recursion

4 ★ | 1 Vote

You should read it

May be interested

  • How to implement a graph data structure in GolangHow to implement a graph data structure in Golang
    charts are one of the essential data structures that you must know as a programmer. let's learn how to create graph/graph data structures in golang !
  • Concept of Buffer in Node.jsConcept of Buffer in Node.js
    net javascript is unicode encoded conveniently but not really good with binary data. when working with tcp streams or file systems, it is necessary to handle octal data streams. node.js provides buffer classes that allow raw data to be stored as an array of integers corresponding to external raw memory allocation v8 heap.
  • Search algorithm by widthSearch algorithm by width
    the breadth search algorithm (breadth first search - bfs for short) walks through a wide graph and uses a queue to memorize adjacent vertices to start the search when no peak is found. adjacent in any loop.
  • How to Implement a Stack Data Structure in C++How to Implement a Stack Data Structure in C++
    a stack is a basic data structure that is commonly used throughout computer science. for example, a stack is utilized by your web browser to remember the last few pages you were on. developers and programmers should be very familiar with...
  • What is Silo Structure? Advantages and disadvantages of silos and effective alternativesWhat is Silo Structure? Advantages and disadvantages of silos and effective alternatives
    everyone knows that a properly structured website is good for both users and seo. silo structure is one of many ways that seo experts recommend people to apply for their website.
  • Deep search algorithmDeep search algorithm
    deep search algorithms (depth first search - dfs for short), also called depth-first search algorithms, are algorithms that browse or search on a tree or graph and use the stack ( stack) to remember adjacent vertices to start the search when the adjacent vertex is not encountered in any loop.
  • Environment settings in Data structuresEnvironment settings in Data structures
    because c and c ++ languages ​​are the languages ​​that almost every university uses to teach, in this chapter i will guide you to install c and c ++ to run the examples in the configuration series. structure and algorithm.
  • What is URL? Structure of the URLWhat is URL? Structure of the URL
    what exactly is a url, what is its structure and composition? this article will give you an overview of urls and its structure.
  • New achievement: TSP chip structure can run 1 million billion operations per secondNew achievement: TSP chip structure can run 1 million billion operations per second
    chips with the tsp structure of startup groq can perform up to 1 peta task per second, that is, 1,000,000,000,000,000 actions per second.
  • Types of data center designTypes of data center design
    it professionals always have to learn, apply new ways to design the data center structure to get efficiency, ensure large capacity and easily expand without any trouble.

Data structure and algorithm