Browse trees in data structures and algorithms

What is browsing trees?

Tree browsing is a process for accessing all the nodes of a tree and can also print the values ​​of these nodes. Because all nodes are connected via edges (or links), we always start accessing from the root node. Therefore, we cannot randomly access any node in the tree. There are three methods that we can use to browse a tree:

Pre-order Traversal

Browse in order (In-order Traversal)

Post-order Traversal (Post-order Traversal)

Generally, we browse a tree to search or to locate the given element or key in the tree or to print all the values ​​that the tree contains.

Browse middle order in binary tree

In this way, the left subtree is accessed first, then the root node and then the right subtree. You should always keep in mind that each node can represent a subtree.

If a binary tree is approved in the middle order, the result will be the key values ​​arranged in ascending order.

Browse trees in data structures and algorithms Picture 1

In the example shown above, A is the root node. With the secondary order-approval method, we start from the root node A, move to the sub-tree to the left of the root node. Here, B is also approved in the way of secondary order approval. And the process continues until all the buttons have been accessed. The result of the central order approval for the above tree will be:

D → B → E → A → F → C → G

Algorithm for how to browse middle order

Duyệt cho tới khi tất cả các nút đều được duyệt: Bước 1 : Duyệt các cây con bên trái một cách đệ qui Bước 2 : Truy cập nút gốc Bước 3 : Duyệt các cây con bên phải một cách đệ qui

Browse money order in binary tree

In the way to browse the order in the binary tree, the root node is first browsed, then the left tree will be browsed and will eventually browse the right subtree.

Browse trees in data structures and algorithms Picture 2

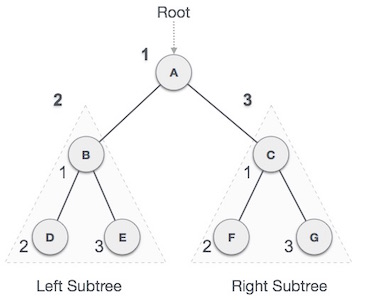
In the example shown above, A is the root node. We start from A, and in the order of pre-order, we first access this root node A and then move to its child node on the left of B. B is also approved in the way of money order approval. And the process continues until all the buttons have been accessed. The result of how to approve the order of this tree will be:

A → B → D → E → C → F → G

Algorithm for how to browse the order

Duyệt cho tới khi tất cả các nút đều được duyệt: Bước 1 : Truy cập nút gốc Bước 2 : Duyệt các cây con bên trái một cách đệ qui Bước 3 : Duyệt các cây con bên phải một cách đệ qui

Browse post-order in binary trees

In the way of browsing the order in the binary tree, the root node of the tree will be last accessed, so you need to pay attention. First, we browse the tree on the left, then browse to the right subtree and finally browse to the root node.

Browse trees in data structures and algorithms Picture 3

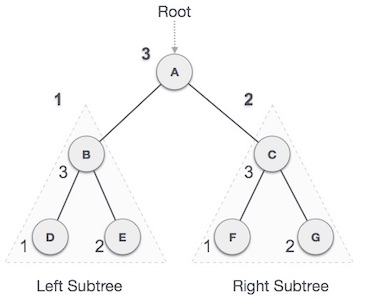
In the example shown above, A is the root node. We start from A, and by way of post-order approval, we first access the subtree on the left B. B is also approved in the second order of post-order approval. And the process will continue until all the nodes have been accessed. The result of the post-order review of the above subtree will be:

D → E → B → F → G → C → A

Algorithm for post-order browsing

Duyệt cho tới khi tất cả các nút đều được duyệt: Bước 1 : Duyệt các cây con bên trái một cách đệ qui Bước 2 : Duyệt các cây con bên phải một cách đệ qui Bước 3 : Truy cập nút gốc.

According to Tutorialspoint

Previous lesson: Search algorithm by width

Next article: Binary Search Tree (Binary Search Tree)