Problem of Hanoi Tower (Tower of Hanoi)

What is Hanoi Tower (Tower of Hanoi)?

Problem of Hanoi Tower (Tower of Hanoi) is a math game consisting of 3 columns and with more disk numbers 1.

Below is an illustration of the Tower of Hanoi problem with 3 discs.

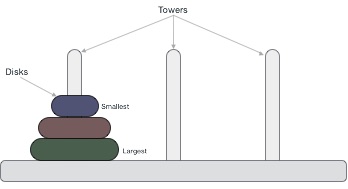
Problem of Hanoi Tower (Tower of Hanoi) Picture 1

The disks are of different sizes and stacked in ascending order to the top-down size: smaller disks are on larger disks. With different disk numbers, we have different Tower of Hanoi problems, but the solutions to these problems are similar. The optimal solution for the Tower of Hanoi problem is when the game has only 3 piles. With a larger number of piles, the solution to the problem is not yet confirmed.

Math game rules of Hanoi Tower (Tower of Hanoi)

The task of the game is to move the disks of different sizes to another column so as to ensure the original order of the disks: the small disk is on the large disk. Here are some rules for the Hanoi Tower math game (Tower of Hanoi):

Only one disk from one column to another can be moved at a time.

Only move the disk at the top (do not move the disks between).
Larger disks cannot be placed on smaller sized discs.

Below is an illustration of how to solve the Tower of Hanoi problem with 3 discs.

Problem of Hanoi Tower (Tower of Hanoi) Picture 2

The problem of Hanoi Tower (Tower of Hanoi) with disk number n can be solved with the minimum number of steps of 2 ⁿ −1 . Therefore, in the case of 3 discs, the Tower of Hanoi problem can be solved after 2 ³ −1 = 7 steps.

Algorithm for Hanoi Tower problem (Tower of Hanoi)

To write an algorithm for the Tower of Hanoi math game, we first need to learn how to solve the problem with the number of disks of 1 and 2. We assign 3 columns with the following names:

cotNguon : the original column contains the disk

cotDich : column to move the disks to

CentralGian : intermediate columns have the purpose of mediating during disk movement

If there is only 1 disk, we only need to move from cotNguon to cotDich.

If there are 2 discs:

First we move the top disk (the smallest disk) to the MiddleGian.

Then we move the disk at the bottom (larger disk) to cotDich.

And finally move the smallest disk from the Chinese version to cotDich.

Problem of Hanoi Tower (Tower of Hanoi) Picture 3

From these two algorithms, we will have an algorithm for the Tower of Hanoi problem for 3 or more discs. We divide the disk stack into two parts: the largest (the nth disk) is the first and (n-1) the other is the second.

Our goal is to move the nth disk from cotNguon to cotDich and then put all the remaining (n-1) disks on it. Now we can imagine how to solve the problem based on recursion according to the following steps:

 Bước 1 : Di chuyển n-1 đĩa từ cotNguon tới cotTrungGian Bước 2 : Di chuyển đĩa thứ n từ cotNguon tới cotDich Bước 3 : Di chuyển n-1 đĩa từ cotTrungGian về cotDich

The recursive algorithm for the Tower of Hanoi problem is:

 B ắ t đầ u gi ả i thu ậ t Th á p H à n ộ i Hanoi ( disk , cotNguon , cotDich , cotTrungGian ) IF disk == 0 , th ì di chuy ể n đĩ a t ừ cotNguon t ớ i cotDich ELSE Hanoi ( disk - 1 , cotNguon , cotTrungGian , cotDich ) // Bước 1 di chuy ể n đĩ a t ừ cotNguon t ớ i cotDich // Bước 2 Hanoi ( disk - 1 , cotTrungGian , cotDich , cotNguon ) // Bước 3 K ế t th ú c IF K ế t th ú c gi ả i thu ậ t

According to Tutorialspoint

Previous article: Basic concepts of recursion

Next lesson: Fibonacci sequence in data structure and algorithm

Lesley Montoya

Update 25 May 2019

You should read it

May be interested

Alignment algorithm (Merge Sort)
mixing (merge sort) is an arrangement algorithm based on the divide and conquer algorithm. with the worst case time complexity of Ο (n log n), this is one of the algorithms that deserves the most attention.
Shell Sort in data structure and algorithm
shell sort is a highly efficient sorting algorithm based on insertion sorting algorithm (insertion sort). this algorithm avoids the case of swapping positions of two distant elements in the selection algorithm (if the smaller element is in the right position quite far from the larger element on the left).
Quick Sort (Quick Sort)
quick sort is a highly efficient algorithm and is based on dividing the array into smaller pieces.
Graph data structure (Graph)
a graph (graph) is a form of visual representation of a set of objects in which pairs of objects are connected by links. interconnected objects are represented by points called vertices, and links that connect vertices are called edges.
Deep search algorithm
deep search algorithms (depth first search - dfs for short), also called depth-first search algorithms, are algorithms that browse or search on a tree or graph and use the stack ( stack) to remember adjacent vertices to start the search when the adjacent vertex is not encountered in any loop.
Search algorithm by width
the breadth search algorithm (breadth first search - bfs for short) walks through a wide graph and uses a queue to memorize adjacent vertices to start the search when no peak is found. adjacent in any loop.