Asymptotic analysis in Data Structures and Algorithms

In the previous chapter, we learned about theoretical analysis and some concepts of time complexity and memory complexity in algorithm analysis. In this chapter, I will discuss Proximity Analysis in Data Structures and Algorithms.

What is proximity analysis?

The asymptotic analysis of an algorithm is a concept that helps us estimate the running time of an algorithm. Using asymptotic analysis, we can draw the best conclusions about the best case scenario, the average case, the worst case of an algorithm. To refer to these cases, you can learn what is the Data Structures chapter?

Asymptotic analysis means approaching input data, ie if the algorithm does not have Input, the final conclusion is that the algorithm will run for a specific amount of time and is constant. In addition to the Input factor, other factors are considered constant.

Asymptotic analysis refers to estimating the running time of any calculation in the calculation steps. For example, the running time of a certain calculation is evaluated as a function f (n) and for another calculation is the function g (n2). This means that the running time of the first calculation will increase linearly with the increase of n and the running time of the second calculation will increase exponentially when n increases. Similarly, when n is quite small, the running time of the two operations is nearly the same.

Usually the time required by an algorithm is divided into 3 categories:

1. Best case : is the smallest time required to execute the program.
2. Average case : is the average time needed to implement the program.
3. Worst case : is the maximum time required to execute the program.

Asymptotic Notation in Data Structures and Algorithms

The following Asymptotic Notation is commonly used in estimating the run-time complexity of an algorithm:

Ation Notation

Ation Notation

ation Notation

Big Oh Notation, Ο in Data Structures and Algorithms

Ο (n) is a way to represent the upper bound of the runtime of an algorithm. It estimates the worst-case time complexity or is the longest amount of time required by an algorithm (executed from start to end). The graph shows as follows:

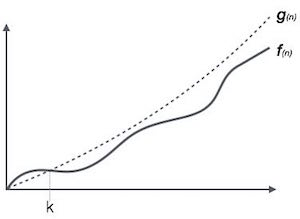
For example, calling f (n) and g (n) are functions that do not reduce the definition on positive integers (all time functions satisfy these conditions):

 Ο( f ( n )) = { g ( n ) : n ế u t ồ n t ạ i c > 0 v à n 0 sao cho g ( n ) ≤ c . f ( n ) v ớ i m ọ i n > n 0 . } 

Omega Notation, Ω in Data structures and algorithms

The Ω (n) is a way to represent the lower bound of an algorithm's runtime. It estimates the best case-time complexity or is the shortest amount of time required by an algorithm. The graph shows as follows:

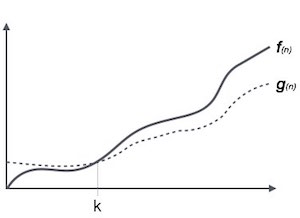
For example, with a function f (n):

 Ω( f ( n )) ≥ { g ( n ) : n ế u t ồ n t ạ i c > 0 v à n 0 sao cho g ( n ) ≤ c . f ( n ) v ớ i m ọ i n > n 0 . } 

Theta Notation, θ in Data structures and algorithms

The θ (n) is a way to represent both the upper and lower bound of the run time of an algorithm. You look at the item:

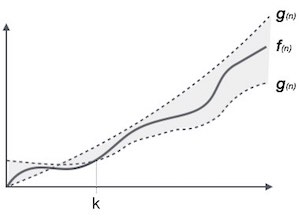
Some Asymptotic Notation is popular in data structures and algorithms

constant - Ο (1)

logarithm - Ο (log n)

Linear (Linear) - Ο (n)

n log n - Ο (n log n)

Quadratic - Ο (n ² )

Tier 3 (cubic) - Ο (n ³ )

Polynomial - n ^{Ο (1)}

Exponential - 2 ^{Ο (n)}

According to Tutorialspoint

Last lesson: What is algorithm?

Next lesson: Greedy Algorithm (Greedy Algorithm)