Matrix in Python

In this article, we will learn about Python matrices using nested lists and the NumPy library.

Matrix is a two-dimensional data structure in which numbers are arranged in rows and columns. For example:

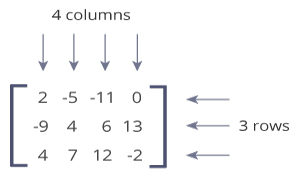
This is a 3x4 matrix because it has 3 rows and 4 columns.

Matrix in Python

Python has no built-in type for matrices, so we can render the matrix as a nested list.

So what is the nested list?

Nested list is a nested list , meaning a list appears as an element of another list. For example:

 A = [ 1, 4, 5, [8, 9]] 

In this example, if you print A [3], the output is [8, 9].

Nested lists are often used to display matrices in Python. Performing as follows:

 A = [[1, 4, 5], 
  [-5, 8, 9]] 

We can consider this list to be a matrix of 2 rows and 3 columns.

In order to derive the element from the matrix, we can either select a row of the matrix in the usual way or use the dual index form, the first number to select the row, while the second indicator selects the column. See the following example:

 A = [[1, 4, 5, 12], 
  [-5, 8, 9, 0], 
  [-6, 7, 11, 19]] 
 
 print("A =", A) 
 print("A[1] =", A[1]) # Hàng thứ 2 của ma trân 
 print("A[1][2] =", A[1][2]) # Phần tử thứ 3 của hàng thứ 2 
 print("A[0][-1] =", A[0][-1]) # Phần tử cuối cùng của hàng 1 
 
 column = []; 
 for row in A: 
  column.append(row[2]) 
 
 print("Cột thứ 3 =", column) 

Run the program, the output returned is:

 A = [[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]] 
 A[1] = [-5, 8, 9, 0] 
 A[1][2] = 9 
 A[0][-1] = 12 
 Cột thứ 3 = [5, 9, 11] 

Using a nested list to represent matrices is a common way and is often used in simple calculations. However, a better way is to use the NumPy library.

Use NumPy for the matrix

NumPy is a library written in Python for scientific calculations, supports multiple data types for multidimensional calculations, programming, working with database systems extremely convenient.

To create a matrix we can use ndarray (abbreviated array) of NumPy

This array is a homogeneous multidimensional array object that means all elements are of the same type.

Try with an example:

 import numpy as np 
 a = np.array([1, 2, 3]) 
 print(a) 
 
 # Output: [1, 2, 3] 
 
 print(type(a)) 
 
 # Output:  

How to create an NumPy array

Integer array, real number, complex number (integer, float, complex)

 import numpy as np 
 
 A = np.array([[1, 2, 3], [3, 4, 5]]) 
 print(A) 
 
 A = np.array([[1.1, 2, 3], [3, 4, 5]]) # mảng số thực 
 print(A) 
 
 A = np.array([[1, 2, 3], [3, 4, 5]], dtype = complex) # mảng số phức 
 print(A) 

The program returns results:

 [[1 2 3] 
  [3 4 5]] 
 
 [[1.1 2. 3. ] 
  [3. 4. 5. ]] 
 
 [[1.+0.j 2.+0.j 3.+0.j] 
  [3.+0.j 4.+0.j 5.+0.j]] 

Default value array (0 and 1)

 import numpy as np 

 # All elements are 0 
 A = np.zeros ((2, 3)) 
 print (A) 

 # Output: 
 [[0. 0. 0.] 
 [0. 0. 0.]] 

 # All elements are 1 
 B = np.ones ((1, 5)) 
 print (B) 

 # Output: [[1 1 1 1 1]] 

Use arange () and shape ()

 import numpy as np 

 A = np.arange (4) 
 print ('A =', A) 

 B = np.arange (12) .reshape (2, 6) 
 print ('B =', B) 

 # Output: 
 A = [0 1 2 3] 
 B = [[0 1 2 3 4 5] 
 [6 7 8 9 10 11]] 

Math operations with matrices

Math operations on matrices are basic calculations when working. In this section, Quantrimang only mentioned three commonly used basic operations: matrix addition, matrix multiplication and matrix displacement.

The operations here use both the nested list and the NumPy library.

Add 2 matrices

To add two matrices, we add each corresponding element of the two matrices at the same level.

 import numpy as np 

 A = np.array ([[2, 4], [5, -6]]) 
 B = np.array ([[9, -3], [3, 6]]) 
 C = A + B 
 print (C) 

 '' ' 
 Output: 
 [[11 1] 
 [8 0]] 
 '' ' 

Multiply 2 matrices

Multiplying 2 matrices is the sum of the sum of each product of the row corresponding to the corresponding column.

Note: Matrix multiplier only occurs when the number of columns of matrix A is equal to the number of rows of matrix B. For example, for 2 matrices [A] mp and [B] pn, their product in that order will be bound The result is the matrix [AB] mn.

Performing with NumPy is as follows:

 import numpy as np 

 A = np.array ([[3, 6, 7], [5, -3, 0]]) 
 B = np.array ([[1, 1], [2, 1], [3, -3]]) 
 C = a.dot (B) 
 print (C) 

 # Output: 
 [[36 -12] 
 [ -twelfth]] 

Transfer matrix

Displacement is the transformation of columns into rows and rows into columns of a matrix.

 import numpy as np 

 A = np.array ([[1, 1], [2, 1], [3, -3]]) 
 print (A.transpose ()) 

 #Output: 
 [[1 2 3] 
 [1 1 -3]] 

Export the elements, columns, lines of the matrix

Export the elements of the matrix

Similar to the way to export by list, we can use using NumPy. First, try the one-dimensional array:

 import numpy as np 
 A = np.array ([12, 14, 16, 18, 20]) 

 print ("A [0] =", A [0]) # first element 
 print ("A [2] =", A [2]) # 3rd element 
 print ("A [-1] =", A [-1]) # the last element 

The output returned here is:

 A[0] = 12 
 A[2] = 16 
 A[-1] = 20 

Example of a two-dimensional array:

 import numpy as np 

 A = np.array ([[1, 4, 5, 12], 
 [-5, 8, 9, 0], 
 [-6, 7, 11, 19]])) 

 # The first element of the first row 
 print ("A [0] [0] =", A [0] [0]) 

 # 3rd element of the second row 
 print ("A [1] [2] =", A [1] [2]) 

 # The last element of the last row 
 print ("A [-1] [- 1] =", A [-1] [- 1]) 

Run the program, the result returned is:

 A[0][0] = 1 
 A[1][2] = 9 
 A[-1][-1] = 19 

Export the lines of the matrix

 import numpy as np 

 A = np.array ([[1, 4, 5, 12], 
 [-2, 8, 6, 14], 
 [-1, 5, 10, 22]])) 

 print ("A [0] =", A [0]) # First line 
 print ("A [2] =", A [2]) # 3rd line 
 print ("A [-1] =", A [-1]) # Last line (3rd line) 

The output returned here is:

 A[0] = [1, 4, 5, 12] 
 A[2] = [-1, 5, 10, 22] 
 A[-1] = [-1, 5, 10, 22] 

Export columns of the matrix

 import numpy as np 

 A = np.array ([[1, 4, 5, 12], 
 [-2, 8, 6, 14], 
 [-1, 5, 10, 22]])) 

 print ("A [:, 0] =", A [:, 0]) # First column 
 print ("A [:, 3] =", A [:, 3]) # 4th column 
 print ("A [:, - 1] =", A [:, - 1]) # Last column (4th column) 

Output is returned:

 A[:,0] = [ 1 -2 -1] 
 A[:,3] = [12 14 22] 
 A[:,-1] = [12 14 22] 

Slice of the Matrix

The slice of a one-dimensional array in NumPy is represented as a list.

 import numpy as np 
 A = np.array([1, 3, 5, 7, 9, 7, 5]) 
 
 # Phần tử thứ tự từ 3 đến 5 
 print(A[2:5]) # Output: [5, 7, 9] 
 
 # Phần tử thứ tự từ 1 đến 4 
 print(A[:-5]) # Output: [1, 3] 
 
 # Phần tử thứ 6 trở đi 
 print(A[5:]) # Output:[7, 5] 
 
 # Lấy cả mảng 
 print(A[:]) # Output:[1, 3, 5, 7, 9, 7, 5] 
 
 # đổi chiều mảng 
 print(A[::-1]) # Output:[5, 7, 9, 7, 5, 3, 1] 

So to cut the matrix, we have the following example:

 import numpy as np 

 A = np.array ([[1, 4, 5, 12, 14], 
 [-5, 8, 9, 0, 17], 
 [-6, 7, 11, 19, 21]]) 

 print (A [: 2,: 4]) # 2 rows, 4 columns 

 '' 'Output: 
 [[1 4 5 12] 
 [-5 8 9 0]] 
 '' ' 

 print (A [: 1,]) # first row, all columns 

 '' 'Output: 
 [[1 4 5 12 14]] 
 '' ' 

 print (A [:, 2]) # all rows and columns 2 

 '' 'Output: 
 [5 9 11] 
 '' ' 

 print (A [:, 2: 5]) # all rows, columns 3 to 5 

 '' 'Output: 
 [[5 12 14] 
 [9 0 17] 
 [11 19 21]] 
 '' ' 

So as you can see, using the NumPy library instead of the nested list makes operations with matrices much easier. Quantrimang recommends that you learn and learn how to use the NumPy library very carefully, especially when using Python to apply for scientific calculations or data analysis.

Good luck!

See more:

1. Array in Python
2. Functions in Python
3. More than 100 Python exercises have solutions (sample code)

Next article: How to use List comprehension in Python